NIM : 2101696973
Session 5
Binary Search Tree
Binary Search Tree :
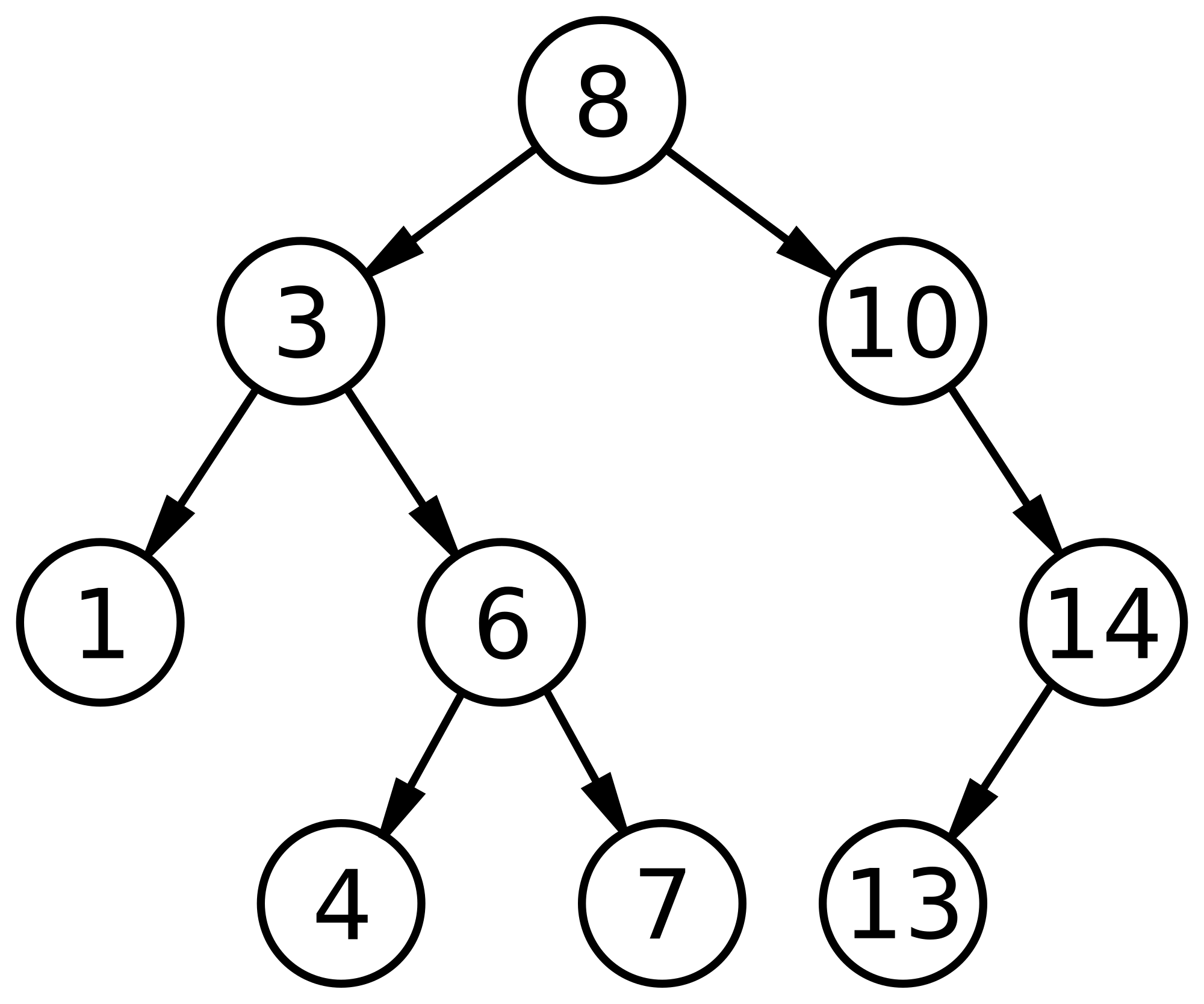
Binary Search Tree(BST) adalah sebuah bentuk data struktur yang menyimpan "barang"(integer angka, char nama, dll) dalam memori. BST mampu melakukan pencarian cepat, penambahan, penghapusan barang, dan dapat digunakan untuk mengimplementasikan set item atau tabel pencarian yang memungkinkan penemuan barang berdasarkan kuncinya (seperti menemukan nomor HP melalui nama orang).BST merupakan sebuah "Rooted Binary Tree", dimana pada tiap node tersimpan sebuah kunci dan juga memiliki 2 "Sub-Tree" biasa dipanggil "Left" and "Right"(kiri dan kanan).
Sering sekali informasi yang direpresentasikan pada tiap node merupakan sebuah rekaman daripada satu data elemen. Namun, untuk kegunaan sequence, node dibandingkan sesuai dengan kunci yang dimiliki mereka daripada bagian manapun yang terikat dengan mereka. Keuntungan paling besar dalam penggunaan BST dibandingkan data struktur lain ialah hal-hal yang berhubungan dengan algoritma sorting dan searching relatif lebih efisien dan juga lebih mudah dikoding.
Operasi Binary Search Tree
BST memiliki operasi dasar ini :
- find(x) : mencari kunci x dalam BST
- insert(x) : memasukkan kunci x baru dalam BST
- remove(x) : menghapus kunci x dalam BST
Operasi Searching
Operasi Searching BST untuk mencari suatu kunci dapat diprogram secara rekursif dan iteratif.
Karena properti dari BST, mencari kunci dalam BST itu mudah.
Misal kunci yang ingin dicari adalah X.
- Dimulai dari root(akar)
- Jika root mengandung X search berhenti dengan suksess
- Jika X kurang dari kunci root, maka search akan rekursif ke Left Sub-tree, sebaliknya jika X lebih dari kunci root search akan ke Right Sub-tree.
struct node*search(struct node*curr,intx){
if(curr==NULL)return NULL;
//X ditemukan
if(X==curr->data)return curr;
//X ada pada Left Sub-tree
if(X<curr->data)return find(curr->left X);
//X ada pada Right Sub-tree
return find(curr->right,X);
}
Operasi Insert
Operasi InsertBinary Searcg Tree(pemasukan data) dilakukan secara rekursif.
Misal Node baru adalah X
- Dimulai dari root
- Jika X kurang dari kunci milik root X pergi ke Left Sub-tree, dan sebaliknya jika X llebih dari kunci milik root
- Diulang sampai ditemukan node kosong untuk menaruh X(X selalu menjadi Leaf baru)
if TREE=NULL, maka
alokasikan memori untuk TREE
set TREE->data=value
set TREE->left=TREE->right=NULL
else
if value<TREE->data
insert(Tree->left,value)
else
insert(Tree->right,value)
misal insert "4"




- 4 kurang dari 5, pergi ke kiri
- 4 lebih dari 2, pergi ke kanan
- 4 lebih dari 3, pergi ke kanan
- 4 sampai pada node kosong dan menjadi Leaf baru
Operasi Deletion
Ada 3 kasus yang harus dipikirkan ketika melakukan Dletion:
- Jika kuncinya merupakan sebuah Leaf, node didelete langsung
- Jika kunci merupakan node yang punya 1 Sub-tree, delete node tersebut dan sambungkan Sub-tree yang tadi pada Parents node yang terdelete
- Jika kunci merupakan node yang memiliki 2 Sub-tree, delete node tersebut dan digantikan dengan anak paling kanan dari Sub-tree kirinya atau anak paling kiri dari Sub-tree kanannya lalu delete anak yang digunakan
if Tree=NULL, maka
tulis "value not found in the tree"
else if value<Tree->data
delete(Tree->left,value)
else if value>Tree->data
delete(Tree->right,value)
else if Tree->left dan Tree->right
set temp=cariNodeTerbesar(Tree->left)
set Tree->data=temp->data
delete(Tree->left,temp->data)
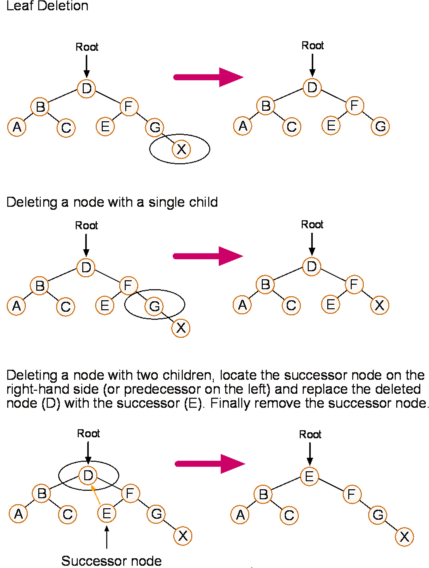
- Bagian pertama menunjukkan delesi dari sebuah Leaf
- Bagian kedua menunjukkan delesi sebuah node dengan 1 anak
- Bagian ketiga menunjukkan dlesi node yang memiliki 2 anak
Sering sekali informasi yang direpresentasikan pada tiap node merupakan sebuah rekaman daripada satu data elemen. Namun, untuk kegunaan sequence, node dibandingkan sesuai dengan kunci yang dimiliki mereka daripada bagian manapun yang terikat dengan mereka. Keuntungan paling besar dalam penggunaan BST dibandingkan data struktur lain ialah hal-hal yang berhubungan dengan algoritma sorting dan searching relatif lebih efisien dan juga lebih mudah dikoding.
Operasi Binary Search Tree
BST memiliki operasi dasar ini :
- find(x) : mencari kunci x dalam BST
- insert(x) : memasukkan kunci x baru dalam BST
- remove(x) : menghapus kunci x dalam BST
Operasi Searching
Operasi Searching BST untuk mencari suatu kunci dapat diprogram secara rekursif dan iteratif.
Karena properti dari BST, mencari kunci dalam BST itu mudah.
Misal kunci yang ingin dicari adalah X.
- Dimulai dari root(akar)
- Jika root mengandung X search berhenti dengan suksess
- Jika X kurang dari kunci root, maka search akan rekursif ke Left Sub-tree, sebaliknya jika X lebih dari kunci root search akan ke Right Sub-tree.
struct node*search(struct node*curr,intx){
if(curr==NULL)return NULL;
//X ditemukan
if(X==curr->data)return curr;
//X ada pada Left Sub-tree
if(X<curr->data)return find(curr->left X);
//X ada pada Right Sub-tree
return find(curr->right,X);
}
Operasi Insert
Operasi InsertBinary Searcg Tree(pemasukan data) dilakukan secara rekursif.
Misal Node baru adalah X
- Dimulai dari root
- Jika X kurang dari kunci milik root X pergi ke Left Sub-tree, dan sebaliknya jika X llebih dari kunci milik root
- Diulang sampai ditemukan node kosong untuk menaruh X(X selalu menjadi Leaf baru)
if TREE=NULL, maka
alokasikan memori untuk TREE
set TREE->data=value
set TREE->left=TREE->right=NULL
else
if value<TREE->data
insert(Tree->left,value)
else
insert(Tree->right,value)
misal insert "4"
- 4 kurang dari 5, pergi ke kiri
- 4 lebih dari 2, pergi ke kanan
- 4 lebih dari 3, pergi ke kanan
- 4 sampai pada node kosong dan menjadi Leaf baru
Operasi Deletion
Ada 3 kasus yang harus dipikirkan ketika melakukan Dletion:
- Jika kuncinya merupakan sebuah Leaf, node didelete langsung
- Jika kunci merupakan node yang punya 1 Sub-tree, delete node tersebut dan sambungkan Sub-tree yang tadi pada Parents node yang terdelete
- Jika kunci merupakan node yang memiliki 2 Sub-tree, delete node tersebut dan digantikan dengan anak paling kanan dari Sub-tree kirinya atau anak paling kiri dari Sub-tree kanannya lalu delete anak yang digunakan
if Tree=NULL, maka
tulis "value not found in the tree"
else if value<Tree->data
delete(Tree->left,value)
else if value>Tree->data
delete(Tree->right,value)
else if Tree->left dan Tree->right
set temp=cariNodeTerbesar(Tree->left)
set Tree->data=temp->data
delete(Tree->left,temp->data)

- Bagian pertama menunjukkan delesi dari sebuah Leaf
- Bagian kedua menunjukkan delesi sebuah node dengan 1 anak
- Bagian ketiga menunjukkan dlesi node yang memiliki 2 anak
Rifqi Amru Bakti-2101696973